Het Vermoeden van Collatz
- Geej se lèllike voel hod!
- I've always felt that blues, rock 'n' roll and country are just about a beat apart. ~ Waylon Jennings
- Vervolgens schoof hij zijn gordijnen opzij en deed een poging naar buiten te zijken
- en als ik dan niet weet wat zeggen, laat ik een boer en doe ik alsof ik moet kotsen
- Er staat "topclub" en dan blijkt het over Anderlecht te gaan. Waar blijven ze die humor toch halen!
- Als je antwoordt, kan Jessica Jaggers Rosenthal je ook bellen en informatie zien zoals je Status Actief en wanneer je chatberichten hebt gelezen.
- Ik denk dat ik moet overgeven.
- er zit stront in de weg
- Afgezaagde reclameslagzinnen heruitgevonden
- mmm. viel mij gisteren plotsklapseling binnen 21 minuten geleden
- Hoe lang duurt een "Het is de week van..."-week op facebook? Drie maanden?
- treinen rijden op rails niet op tijd
- Jeuk en niet tevreden over een uitslag? Klacht indienen!
- als je ja handen wast, blijven je voeten vuil
- Ik ben met mijn gat in de boter gevallen. Nu zit er een haar in de boter.
- Verknoei je tijd op een nuttige manier!
Wiskunde is tof!
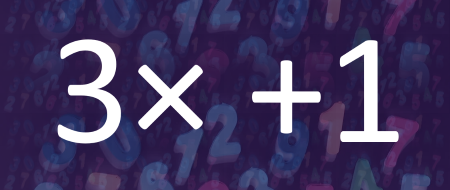
De Duitse wiskundige Lothar Collatz bedacht in 1937 deze mysterieuze getaltheorie, waarbij ongeacht welk startgetal je neemt, de volledige berekening altijd op 1 uitkomt.
De volgende formule wordt gehanteerd: als je startgetal onpaar is wordt dit met 3 vermenigvuldigd en wordt er 1 bijgeteld. Is het getal paar, dan wordt het door 2 gedeeld. Deze formule herhaalt zichzelf tot men op 1 uitkomt.
Volgens Collatz is het niet mogelijk om niet op 1 uit te komen.
Zoals elders vermeld op deze site zijn we eropuit om te proberen allerhande berekeningen, formules, spelletjes en andere dingen in scriptjes te gieten. We zijn er, na niet zo lang klooien en prutsen, uit geraakt. Ongetwijfeld zal er wel een accuratere manier zijn om dit uit te voeren maar we zijn maar hobbyisten en autodidact programmeurs. Het werkt en dat is wat telt!
Het getal wat tot nu toe het dichtst bij het eigen aantal berekeningen ligt, is 19, met 20 stappen.
Laat de magie gebeuren!
Geef in onderstaand formuliertje een getal naar keuze in en Eluterius berekent de hele trip naar het cijfer 1.Statistiekjes... yeah!!
Er zijn reeds 831 startgetallen ingegeven. We kunnen nu natuurlijk allerlei dingen doen met de statistiekjes en berekeningen. Zoals bijvoorbeeld de startgetallen groeperen per aantal stappen. Deze lijst toont de 50 meest voorkomende reeksen van stappen, met de getallen die deze stappen genereren erbij, en het aantal keren dat dit aantal stappen gegenereerd werd. Er zijn tot nu toe 209 verschillende aantal stappen gegenereerd. Het laagst aantal stappen is 1, het hoogst is 567.
STARTGETAL
×
30
86, 87, 89, 520, 522, 524, 525, 528, 529, 532, 533, 536, 538, 555, 571, 577, 578, 579, 583, 633, 635, 20000,
22
28
130, 131, 132, 133, 134, 788, 789, 792, 794, 800, 808, 810, 866, 867, 868, 869, 883, 950, 951, 955, 5005,
21
25
98, 99, 100, 101, 102, 576, 592, 596, 597, 642, 643, 648, 650, 652, 653, 713,
16
36
153, 156, 157, 158, 912, 916, 917, 920, 922, 930, 931, 948, 952, 971, 1025,
15
118
97, 580, 581, 582, 584, 586, 587, 588, 589, 123555, 744556, 756423, 797997, 4807772, 26082023,
15
129
913, 914, 915, 918, 919, 921, 924, 925, 926, 929, 935, 940, 959, 42424242,
14
22
72, 74, 76, 77, 81, 480, 482, 483, 488, 490, 497, 534, 535, 537,
14
39
203, 209, 210, 211, 1224, 1256, 1265, 7445, 7468, 7552, 7896, 9004, 9005, 9006,
14
20
18, 19, 112, 116, 117, 120, 122, 720, 744, 753, 802, 804, 806,
13
23
25, 144, 148, 149, 152, 154, 162, 163, 928, 936, 938, 960, 964,
13
126
684, 685, 686, 689, 690, 691, 694, 695, 697, 707, 25000, 855855,
12
48
481, 489, 492, 493, 494, 498, 499, 508, 509, 510, 539, 3000,
12
33
114, 118, 119, 688, 692, 693, 696, 698, 710, 712, 777, 4444,
12
43
540, 541, 542, 545, 551, 556, 557, 574, 575, 606, 20202, 22000,
12
56
569, 585, 590, 591, 601, 636, 637, 638, 3600, 23000, 745698,
11
31
172, 173, 174, 177, 178, 179, 1111, 1266, 1267, 40000, 45889,
11
15
22, 23, 136, 138, 140, 141, 150, 151, 832, 904, 909,
11
21
36, 37, 38, 224, 232, 234, 240, 241, 244, 245, 8960,
11
26
33, 196, 197, 198, 200, 202, 204, 205, 217, 8552,
10
17
14, 15, 88, 90, 92, 93, 544, 552, 554, 602,
10
38
105, 631, 632, 634, 647, 683, 687, 3950, 4111, 150922,
10
18
28, 29, 30, 176, 180, 181, 184, 186, 201,
9
51
641, 657, 658, 659, 676, 677, 678, 718, 719,
9
27
65, 66, 67, 400, 404, 405, 408, 410, 433,
9
113
108, 109, 110, 656, 660, 666, 674, 675, 4000,
9
41
135, 139, 812, 813, 818, 844, 910, 911, 6006,
9
12
17, 96, 104, 106, 113, 640, 672, 680, 682,
9
19
9, 56, 58, 60, 61, 369, 401, 402, 403,
9
116
145, 146, 147, 872, 884, 885, 899, 903, 927,
9
54
159, 855, 877, 900, 901, 902, 956, 957,
8
14
11, 68, 69, 70, 75, 426, 452, 453,
8
123
514, 515, 516, 517, 518, 521, 530, 531,
8
13
34, 35, 192, 208, 212, 213, 226, 227,
8
111
27, 164, 166, 1000, 6174, 1234567, 1255555,
7
44
185, 187, 191, 1212, 8002, 8030, 40404,
7
34
39, 228, 229, 230, 236, 237, 238,
7
40
406, 407, 409, 420, 421, 422, 455,
7
35
78, 79, 456, 458, 477, 507, 513,
7
61
505, 511, 519, 566, 567, 123456, 680777,
7
110
82, 83, 496, 500, 501, 504, 506,
7
120
399, 2344, 14144, 85546, 86552, 88996,
6
114
216, 218, 220, 221, 8000, 45896,
6
64
673, 679, 681, 699, 711, 755,
6
9
12, 13, 80, 84, 85, 512,
6
105
94, 95, 568, 570, 572, 573,
6
16
7, 44, 45, 46, 301, 302,
6
100
107, 644, 645, 646, 651, 808080,
6
49
169, 963, 986, 988, 999, 5899,
6
72
799, 888, 892, 4785, 5366, 5369,
6
46
123, 127, 735, 764, 809, 4597,
6
Er kan nog meer met deze gegevens gedaan worden.
We kunnen al stellen dat een groter startgetal niet altijd automatisch een groter aantal stappen genereert. En dat er regelmatig drie of vijf opeenvolgende getallen, een gelijk aantal stappen genereren. Zie grafiekje:
Startgetal
Aantal stappen
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
301
302
303
314
333
335
347
365
369
374
380
381
399
400
401
402
403
404
405
406
407
408
409
410
414
417
420
421
422
426
427
432
433
444
452
453
455
456
457
458
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
549
550
551
552
553
554
555
556
557
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
601
602
606
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
666
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
707
710
711
712
713
718
719
720
733
735
744
753
755
764
777
788
789
790
791
792
793
794
795
796
797
798
799
800
802
804
806
808
809
810
811
812
813
818
822
829
832
844
855
865
866
867
868
869
871
872
877
883
884
885
888
892
899
900
901
902
903
904
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
940
948
950
951
952
955
956
957
959
960
963
964
971
986
988
999
1000
1025
1028
1030
1033
1111
1212
1224
1231
1256
1265
1266
1267
1308
1466
1515
1770
1793
1935
1940
1950
1970
1980
1985
2022
2111
2344
2698
2828
3000
3590
3600
3950
3951
4000
4111
4321
4444
4450
4597
4785
4822
4899
5005
5366
5369
5513
5899
6006
6174
6254
6303
6351
6500
7445
7468
7552
7854
7896
7965
8000
8002
8008
8030
8088
8466
8552
8566
8960
9000
9001
9004
9005
9006
9007
9266
9466
9566
9774
9776
9998
10000
10001
10101
10466
11000
12000
12030
12345
13000
14000
14144
15000
19998
19999
20000
20001
20002
20022
20202
22000
23000
25000
30000
30303
36611
36614
36698
38544
40000
40044
40404
45889
45896
47585
47965
50000
50505
51000
55123
55555
55896
60000
60066
60606
70000
70077
70707
74444
75541
77007
77777
78844
80777
80808
82829
85523
85546
86552
87552
87654
87887
88874
88996
89644
90909
96000
99889
100000
110022
123456
123555
142753
150922
157986
202020
250000
400000
411257
413669
444111
444125
445047
445789
522522
666666
666888
680777
684405
744556
745698
753753
753869
756423
797997
808080
855423
855855
866532
875421
888777
951951
974452
986532
998855
1000000
1010122
1111113
1234567
1255555
1414141
1478963
2222355
3030303
4000000
4114112
4141123
4551223
4807772
6654247
7455845
7554554
7777777
8077711
8552314
8996633
9070077
11011963
11111112
12345679
12366555
12369874
15091970
15092022
26082023
40203050
41222589
42424242
52525678
72223568
74222561
78556662
78954566
88888888
89963214
123456789
147852369
321456987
400400400
411111124
412223698
444555666
456888881
495545047
741258963
789654123
877451221
888555222
899899654
989655894
999999999
1223334444
1454777778
3366998877
4545454566
4545871131
8984464687
12345678910
12345678911
77455551255
414141412586
414141412587
444111222555
955545454511
4141414125870
100000000000000
123456789876543
555555555555555
666666666666666
777777777777777
888888888888888
999999999999999
Links
Rechts