Het Vermoeden van Collatz
- Geej se lèllike voel hod!
- Ze hebben mij gekozen omwille van mijn acteertalent en niet omdat ik toevallig een lief snoetje heb ~ Koen WautersTijdens een interview over de film "Intensive Care"...
- Angstschreeuw 8 medeklinkers na elkaar .
- daar durf ik gerust de handen van mijn moeder voor in't vuur te steken!
- Heej Albrecht wij lachen met Anderlecht! Heej ja heej ja hooow!
- amononinium fonium
- Niet dat ik elke dag rondloop als een wandelende stinkwolk
- 13rat13: geel voor die keeper vinnek gwn voor komidie
- beter 10 ballen in de lucht dan euneuch van de keizer te zijn
- Terug de teleurstelling, vernederin en slaag gehandgehaafd
- het is niet alles koek en ei wat blinkt
- THAT'S NOT MICKEY MOUSE, THAT'S TIT DIRT!!!
- hoeren zien en zwijgen
- Kitsenkits = braakbal van een kat
- dit zijn de ontwikkelingen die ervoor zorgen dat dysieke winkels failliet gaan
- Verknoei je tijd op een nuttige manier!
Wiskunde is tof!
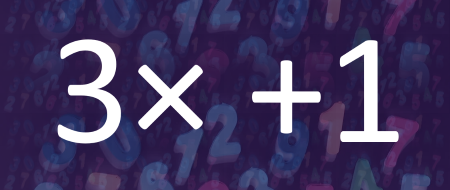
De Duitse wiskundige Lothar Collatz bedacht in 1937 deze mysterieuze getaltheorie, waarbij ongeacht welk startgetal je neemt, de volledige berekening altijd op 1 uitkomt.
De volgende formule wordt gehanteerd: als je startgetal onpaar is wordt dit met 3 vermenigvuldigd en wordt er 1 bijgeteld. Is het getal paar, dan wordt het door 2 gedeeld. Deze formule herhaalt zichzelf tot men op 1 uitkomt.
Volgens Collatz is het niet mogelijk om niet op 1 uit te komen.
Zoals elders vermeld op deze site zijn we eropuit om te proberen allerhande berekeningen, formules, spelletjes en andere dingen in scriptjes te gieten. We zijn er, na niet zo lang klooien en prutsen, uit geraakt. Ongetwijfeld zal er wel een accuratere manier zijn om dit uit te voeren maar we zijn maar hobbyisten en autodidact programmeurs. Het werkt en dat is wat telt!
Het getal wat tot nu toe het dichtst bij het eigen aantal berekeningen ligt, is 19, met 20 stappen.
Laat de magie gebeuren!
Geef in onderstaand formuliertje een getal naar keuze in en Eluterius berekent de hele trip naar het cijfer 1.Statistiekjes... yeah!!
Er zijn reeds 831 startgetallen ingegeven. We kunnen nu natuurlijk allerlei dingen doen met de statistiekjes en berekeningen. Zoals bijvoorbeeld de startgetallen groeperen per aantal stappen. Deze lijst toont de 50 meest voorkomende reeksen van stappen, met de getallen die deze stappen genereren erbij, en het aantal keren dat dit aantal stappen gegenereerd werd. Er zijn tot nu toe 209 verschillende aantal stappen gegenereerd. Het laagst aantal stappen is 1, het hoogst is 567.
STARTGETAL
×
30
86, 87, 89, 520, 522, 524, 525, 528, 529, 532, 533, 536, 538, 555, 571, 577, 578, 579, 583, 633, 635, 20000,
22
28
130, 131, 132, 133, 134, 788, 789, 792, 794, 800, 808, 810, 866, 867, 868, 869, 883, 950, 951, 955, 5005,
21
25
98, 99, 100, 101, 102, 576, 592, 596, 597, 642, 643, 648, 650, 652, 653, 713,
16
118
97, 580, 581, 582, 584, 586, 587, 588, 589, 123555, 744556, 756423, 797997, 4807772, 26082023,
15
36
153, 156, 157, 158, 912, 916, 917, 920, 922, 930, 931, 948, 952, 971, 1025,
15
129
913, 914, 915, 918, 919, 921, 924, 925, 926, 929, 935, 940, 959, 42424242,
14
22
72, 74, 76, 77, 81, 480, 482, 483, 488, 490, 497, 534, 535, 537,
14
39
203, 209, 210, 211, 1224, 1256, 1265, 7445, 7468, 7552, 7896, 9004, 9005, 9006,
14
20
18, 19, 112, 116, 117, 120, 122, 720, 744, 753, 802, 804, 806,
13
23
25, 144, 148, 149, 152, 154, 162, 163, 928, 936, 938, 960, 964,
13
48
481, 489, 492, 493, 494, 498, 499, 508, 509, 510, 539, 3000,
12
33
114, 118, 119, 688, 692, 693, 696, 698, 710, 712, 777, 4444,
12
43
540, 541, 542, 545, 551, 556, 557, 574, 575, 606, 20202, 22000,
12
126
684, 685, 686, 689, 690, 691, 694, 695, 697, 707, 25000, 855855,
12
15
22, 23, 136, 138, 140, 141, 150, 151, 832, 904, 909,
11
21
36, 37, 38, 224, 232, 234, 240, 241, 244, 245, 8960,
11
56
569, 585, 590, 591, 601, 636, 637, 638, 3600, 23000, 745698,
11
31
172, 173, 174, 177, 178, 179, 1111, 1266, 1267, 40000, 45889,
11
38
105, 631, 632, 634, 647, 683, 687, 3950, 4111, 150922,
10
26
33, 196, 197, 198, 200, 202, 204, 205, 217, 8552,
10
17
14, 15, 88, 90, 92, 93, 544, 552, 554, 602,
10
12
17, 96, 104, 106, 113, 640, 672, 680, 682,
9
19
9, 56, 58, 60, 61, 369, 401, 402, 403,
9
116
145, 146, 147, 872, 884, 885, 899, 903, 927,
9
18
28, 29, 30, 176, 180, 181, 184, 186, 201,
9
51
641, 657, 658, 659, 676, 677, 678, 718, 719,
9
27
65, 66, 67, 400, 404, 405, 408, 410, 433,
9
41
135, 139, 812, 813, 818, 844, 910, 911, 6006,
9
113
108, 109, 110, 656, 660, 666, 674, 675, 4000,
9
123
514, 515, 516, 517, 518, 521, 530, 531,
8
13
34, 35, 192, 208, 212, 213, 226, 227,
8
54
159, 855, 877, 900, 901, 902, 956, 957,
8
14
11, 68, 69, 70, 75, 426, 452, 453,
8
61
505, 511, 519, 566, 567, 123456, 680777,
7
110
82, 83, 496, 500, 501, 504, 506,
7
111
27, 164, 166, 1000, 6174, 1234567, 1255555,
7
44
185, 187, 191, 1212, 8002, 8030, 40404,
7
34
39, 228, 229, 230, 236, 237, 238,
7
40
406, 407, 409, 420, 421, 422, 455,
7
35
78, 79, 456, 458, 477, 507, 513,
7
9
12, 13, 80, 84, 85, 512,
6
16
7, 44, 45, 46, 301, 302,
6
105
94, 95, 568, 570, 572, 573,
6
100
107, 644, 645, 646, 651, 808080,
6
49
169, 963, 986, 988, 999, 5899,
6
72
799, 888, 892, 4785, 5366, 5369,
6
46
123, 127, 735, 764, 809, 4597,
6
120
399, 2344, 14144, 85546, 86552, 88996,
6
114
216, 218, 220, 221, 8000, 45896,
6
64
673, 679, 681, 699, 711, 755,
6
Er kan nog meer met deze gegevens gedaan worden.
We kunnen al stellen dat een groter startgetal niet altijd automatisch een groter aantal stappen genereert. En dat er regelmatig drie of vijf opeenvolgende getallen, een gelijk aantal stappen genereren. Zie grafiekje:
Startgetal
Aantal stappen
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Dit zijn 50 berekeningen van de ingegeven 831 getallen. Om de hele lijst te zien klik hier.
Links
Rechts